Common infrastructure

exception meshmode.Error

exception meshmode.DataUnavailable

exception meshmode.FileExistsError

exception meshmode.InconsistentVerticesError

class meshmode.AffineMap(matrix=None, offset=None)

An affine map A@x+b represented by a matrix A and an offset vector b.

matrix

A numpy.ndarray representing the matrix A, or None.

offset

A numpy.ndarray representing the vector b, or None.

__init__(matrix=None, offset=None)

Parameters:

• matrix – A numpy.ndarray (or something convertible to one), or None.

• offset – A numpy.ndarray (or something convertible to one), or None.

inverted()

Return the inverse affine map.

__call__(vecs)

Apply the affine map to an array vecs whose first axis length matches matrix.shape[1].

__eq__(other)

Return self==value.

__ne__(other)

Return self!=value.

Mesh management

Design of the Data Structure

Why does a Mesh need to be broken into MeshElementGroup instances?

Elements can be of different types (e.g. triangle, quadrilateral, tetrahedron, what have you). In addition, elements may vary in the polynomial degree used to represent them (see also below).

All these bits of information could in principle be stored by element, but having large, internally homogeneous groups is a good thing from an efficiency standpoint. (So that you can, e.g., launch one GPU kernel to deal with all order-3 triangles, instead of maybe having to dispatch based on type and size inside the kernel)

What is the difference between ‘vertices’ and ‘nodes’?

Nodes exist mainly to represent the (potentially non-affine) deformation of each element, by a one-to-one correspondence with MeshElementGroup.unit_nodes. They are unique to each element. Vertices on the other hand exist to clarify whether or not a point shared by two elements is actually identical (or just happens to be “close”). This is done by assigning (single, globally shared) vertex numbers and having elements refer to them.

Consider the following picture:

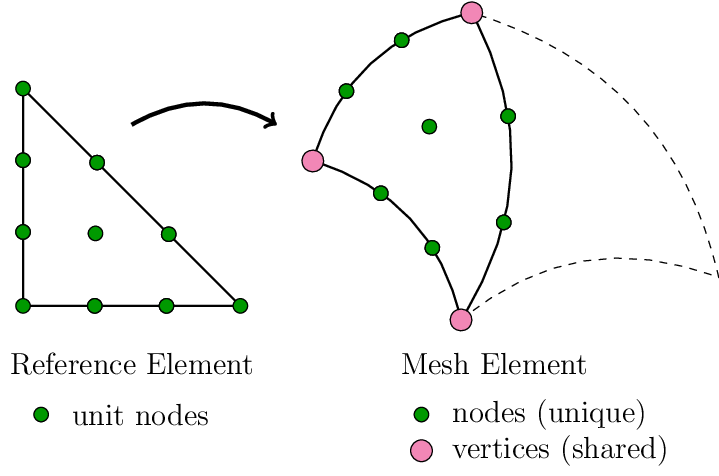
Mesh nodes and vertices

Mesh Data Structure

class meshmode.mesh.MeshElementGroup(order: int, vertex_indices: Optional[ndarray], nodes: ndarray, unit_nodes: Optional[ndarray] = None, element_nr_base: Optional[int] = None, node_nr_base: Optional[int] = None, _factory_constructed: bool = False)

A group of elements sharing a common reference element.

order

The maximum degree used for interpolation. The exact meaning depends on the element type, e.g. for SimplexElementGroup this is the total degree.

dim

The number of dimensions spanned by the element. Not the ambient dimension, see Mesh.ambient_dim for that.

nvertices

Number of vertices in the reference element.

nfaces

Number of faces of the reference element.

nunit_nodes

Number of nodes on the reference element.

nelements

Number of elements in the group.

nnodes

Total number of nodes in the group (equivalent to nelements * nunit_nodes).

vertex_indices

An array of shape (nelements, nvertices) of (mesh-wide) vertex indices.

nodes

An array of node coordinates with shape (mesh.ambient_dim, nelements, nunit_nodes).

unit_nodes

An array with shape (dim, nunit_nodes) of nodes on the reference element. The coordinates nodes are a mapped version of these reference nodes.

is_affine

A bool flag that is True if the local-to-global parametrization of all the elements in the group is affine.

Element groups can also be compared for equality using the following methods. Note that these are very expensive, as they compare all the nodes.

__eq__(other)

Return self==value.

__ne__(other)

Return self!=value.

__init__(order: int, vertex_indices: Optional[ndarray], nodes: ndarray, unit_nodes: Optional[ndarray] = None, element_nr_base: Optional[int] = None, node_nr_base: Optional[int] = None, _factory_constructed: bool = False) → None

The following abstract methods must be implemented by subclasses.

abstract classmethod make_group(**kwargs: Any) → MeshElementGroup

Instantiate a new group of class cls.

Unlike the constructor, this factory function performs additional consistency checks and should be used instead.

abstract face_vertex_indices() → Tuple[Tuple[int, ...], ...]

Returns:

a tuple of tuples indicating which vertices (in mathematically positive ordering) make up each face of an element in this group.

abstract vertex_unit_coordinates() → ndarray

Returns:

an array of shape (nfaces, dim) with the unit coordinates of each vertex.

class meshmode.mesh.SimplexElementGroup(order: int, vertex_indices: Optional[ndarray], nodes: ndarray, unit_nodes: Optional[ndarray] = None, element_nr_base: Optional[int] = None, node_nr_base: Optional[int] = None, _factory_constructed: bool = False, dim: Optional[int] = None, _modepy_shape: Optional[Shape] = None, _modepy_space: Optional[FunctionSpace] = None)

Inherits from MeshElementGroup.

class meshmode.mesh.TensorProductElementGroup(order: int, vertex_indices: Optional[ndarray], nodes: ndarray, unit_nodes: Optional[ndarray] = None, element_nr_base: Optional[int] = None, node_nr_base: Optional[int] = None, _factory_constructed: bool = False, dim: Optional[int] = None, _modepy_shape: Optional[Shape] = None, _modepy_space: Optional[FunctionSpace] = None)

Inherits from MeshElementGroup.

class meshmode.mesh.Mesh(vertices, groups, *, skip_tests=False, node_vertex_consistency_tolerance=None, skip_element_orientation_test=False, nodal_adjacency=None, facial_adjacency_groups=None, vertex_id_dtype=<class 'numpy.int32'>, element_id_dtype=<class 'numpy.int32'>, is_conforming=None)

ambient_dim

dim

vertices

None or an array of vertex coordinates with shape (ambient_dim, nvertices). If None, vertices are not known for this mesh.

nvertices

groups

A list of MeshElementGroup instances.

nelements

base_element_nrs

An array of size (len(groups),) of starting element indices for each group in the mesh.

base_node_nrs

An array of size (len(groups),) of starting node indices for each group in the mesh.

nodal_adjacency

An instance of NodalAdjacency.

Referencing this attribute may raise meshmode.DataUnavailable.

facial_adjacency_groups

A list of lists of instances of FacialAdjacencyGroup.

facial_adjacency_groups[igrp] gives the facial adjacency relations for group igrp, expressed as a list of FacialAdjacencyGroup instances.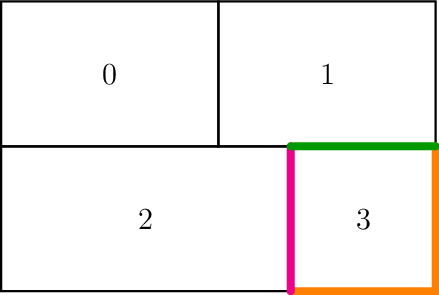

Referencing this attribute may raise meshmode.DataUnavailable.

Facial Adjacency Group

For example for the mesh in the figure, the following data structure could be present:

[
    [...],  # connectivity for group 0
    [...],  # connectivity for group 1
    [...],  # connectivity for group 2
    # connectivity for group 3
    [
        # towards group 1, green
        InteriorAdjacencyGroup(ineighbor_group=1, ...),
        # towards group 2, pink
        InteriorAdjacencyGroup(ineighbor_group=2, ...),
        # towards the boundary, orange
        BoundaryAdjacencyGroup(...)
    ]
]

(Note that element groups are not necessarily geometrically contiguous like the figure may suggest.)

vertex_id_dtype

element_id_dtype

is_conforming

True if it is known that all element interfaces are conforming. False if it is known that some element interfaces are non-conforming. None if neither of the two is known.

copy(**kwargs)

__eq__(other)

Return self==value.

__ne__(other)

Return self!=value.

class meshmode.mesh.NodalAdjacency(neighbors_starts: ndarray, neighbors: ndarray)

Describes nodal element adjacency information, i.e. information about elements that touch in at least one point.

neighbors_starts

element_id_t [nelements+1]

Use together with neighbors. neighbors_starts[iel] and neighbors_starts[iel+1] together indicate a ranges of element indices neighbors which are adjacent to iel.

neighbors

element_id_t []

See neighbors_starts.

__eq__(other)

Return self==value.

__ne__(other)

Return self!=value.

class meshmode.mesh.FacialAdjacencyGroup(igroup: int)

Describes facial element adjacency information for one MeshElementGroup, i.e. information about elements that share (part of) a face or elements that lie on a boundary.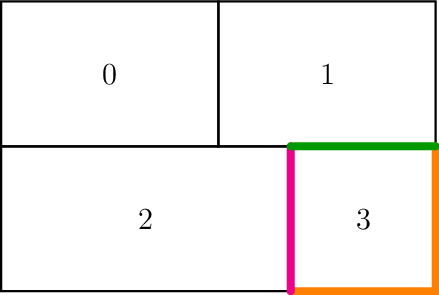

Facial Adjacency Group

Represents (for example) one of the (colored) interfaces between MeshElementGroup instances, or an interface between MeshElementGroup and a boundary. (Note that element groups are not necessarily contiguous like the figure may suggest.)

igroup

class meshmode.mesh.InteriorAdjacencyGroup(igroup: int, ineighbor_group: int, elements: ndarray, element_faces: ndarray, neighbors: ndarray, neighbor_faces: ndarray, aff_map: AffineMap)

Describes interior facial element adjacency information for one MeshElementGroup.

igroup

The mesh element group number of this group.

ineighbor_group

ID of neighboring group, or None for boundary faces. If identical to igroup, then this contains the self-connectivity in this group.

elements

element_id_t [nfagrp_elements]. elements[i] gives the element number within igroup of the interior face.

element_faces

face_id_t [nfagrp_elements]. element_faces[i] gives the face index of the interior face in element elements[i].

neighbors

element_id_t [nfagrp_elements]. neighbors[i] gives the element number within ineighbor_group of the element opposite elements[i].

neighbor_faces

face_id_t [nfagrp_elements]. neighbor_faces[i] gives the face index of the opposite face in element neighbors[i]

aff_map

An AffineMap representing the mapping from the group’s faces to their corresponding neighbor faces.

__eq__(other)

Return self==value.

__ne__(other)

Return self!=value.

class meshmode.mesh.BoundaryAdjacencyGroup(igroup: int, boundary_tag: Hashable, elements: ndarray, element_faces: ndarray)

Describes boundary adjacency information for one MeshElementGroup.

igroup

The mesh element group number of this group.

boundary_tag

The boundary tag identifier of this group.

elements

element_id_t [nfagrp_elements]. elements[i] gives the element number within igroup of the boundary face.

element_faces

face_id_t [nfagrp_elements]. element_faces[i] gives the face index of the boundary face in element elements[i].

class meshmode.mesh.InterPartAdjacencyGroup(igroup: int, boundary_tag: Hashable, elements: ndarray, element_faces: ndarray, part_id: Hashable, neighbors: ndarray, neighbor_faces: ndarray, aff_map: AffineMap)

Describes inter-part adjacency information for one MeshElementGroup.

igroup

The mesh element group number of this group.

boundary_tag

The boundary tag identifier of this group. Will be an instance of BTAG_PARTITION.

part_id

The identifier of the neighboring part.

elements

Group-local element numbers. Element element_id_dtype elements[i] and face face_id_dtype element_faces[i] is connected to neighbor element element_id_dtype neighbors[i] with face face_id_dtype neighbor_faces[i].

element_faces

face_id_dtype element_faces[i] gives the face of element_id_dtype elements[i] that is connected to neighbors[i].

neighbors

element_id_dtype neighbors[i] gives the volume element number within the neighboring part of the element connected to element_id_dtype elements[i] (which is a boundary element index). Use ~meshmode.mesh.processing.find_group_indices to find the group that the element belongs to, then subtract element_nr_base to find the element of the group.

neighbor_faces

face_id_dtype global_neighbor_faces[i] gives face index within the neighboring part of the face connected to element_id_dtype elements[i]

aff_map

An AffineMap representing the mapping from the group’s faces to their corresponding neighbor faces.

New in version 2017.1.

meshmode.mesh.as_python(mesh, function_name='make_mesh')

Return a snippet of Python code (as a string) that will recreate the mesh given as an input parameter.

meshmode.mesh.is_true_boundary(boundary_tag)

meshmode.mesh.mesh_has_boundary(mesh, boundary_tag)

meshmode.mesh.check_bc_coverage(mesh, boundary_tags, incomplete_ok=False, true_boundary_only=True)

Verify boundary condition coverage.

Given a list of boundary tags as boundary_tags, this function verifies that

1. the union of all these boundaries gives the complete boundary, 1. all these boundaries are disjoint.

Parameters:

• incomplete_ok – Do not report an error if some faces are not covered by the boundary conditions.

• true_boundary_only – only verify for faces whose tags do not inherit from BTAG_NO_BOUNDARY.

meshmode.mesh.is_boundary_tag_empty(mesh, boundary_tag)

Return True if the corresponding boundary tag does not occur as part of mesh.

Predefined Boundary tags

class meshmode.mesh.BTAG_NONE

A boundary tag representing an empty boundary or volume.

class meshmode.mesh.BTAG_ALL

A boundary tag representing the entire boundary or volume.

In the case of the boundary, BTAG_ALL does not include rank boundaries, or, more generally, anything tagged with BTAG_NO_BOUNDARY.

In the case of a mesh representing an element-wise subset of another, BTAG_ALL does not include boundaries induced by taking the subset. Instead, these boundaries will be tagged with BTAG_INDUCED_BOUNDARY.

class meshmode.mesh.BTAG_REALLY_ALL

A boundary tag representing the entire boundary.

Unlike BTAG_ALL, this includes rank boundaries, or, more generally, everything tagged with BTAG_NO_BOUNDARY.

In the case of a mesh representing an element-wise subset of another, this tag includes boundaries induced by taking the subset, or, more generally, everything tagged with BTAG_INDUCED_BOUNDARY

class meshmode.mesh.BTAG_NO_BOUNDARY

A boundary tag indicating that this edge should not fall under BTAG_ALL. Among other things, this is used to keep rank boundaries out of BTAG_ALL.

class meshmode.mesh.BTAG_PARTITION(part_id: Hashable, part_nr=None)

A boundary tag indicating that this edge is adjacent to an element of another Mesh. The part identifier of the adjacent mesh is given by part_id.

part_id

New in version 2017.1.

class meshmode.mesh.BTAG_INDUCED_BOUNDARY

When a Mesh is created as an element-by-element subset of another (as, for example, when using the Firedrake interop features while passing restrict_to_boundary), boundaries may arise where there were none in the original mesh. This boundary tag is used to indicate such boundaries.

Mesh generation

Curves

meshmode.mesh.generation.make_curve_mesh(curve_f: Callable[[ndarray], ndarray], element_boundaries: ndarray, order: int, *, unit_nodes: Optional[ndarray] = None, node_vertex_consistency_tolerance: Optional[Union[float, bool]] = None, closed: bool = True, return_parametrization_points: bool = False) → Mesh

Parameters:

• curve_f – parametrization for a curve, accepting a vector of point locations and returning an array of shape (2, npoints).

• element_boundaries – a vector of element boundary locations in \([0, 1]\), in order. \(0\) must be the first entry, \(1\) the last one.

• order – order of the (simplex) elements. If unit_nodes is also provided, the orders should match.

• unit_nodes – if given, the unit nodes to use. Must have shape (2, nnodes).

• node_vertex_consistency_tolerance – passed to the Mesh constructor. If False, no checks are performed.

• closed – if True, the curve is assumed closed and the first and last of the element_boundaries must match.

• return_parametrization_points – if True, the parametrization points at which all the nodes in the mesh were evaluated are also returned.

Returns:

a Mesh, or if return_parametrization_points is True, a tuple (mesh, par_points), where par_points is an array of parametrization points.

Curve parametrizations

meshmode.mesh.generation.circle(t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

meshmode.mesh.generation.ellipse(aspect_ratio: float, t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

meshmode.mesh.generation.cloverleaf(t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

meshmode.mesh.generation.starfish

meshmode.mesh.generation.drop(t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

meshmode.mesh.generation.n_gon(n_corners, t)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

meshmode.mesh.generation.qbx_peanut(t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

meshmode.mesh.generation.apple(a: float, t: ndarray)

Parameters:

• a – roundness parameter in \([0, 1/2]\), where \(0\) gives a circle and \(1/2\) gives a cardioid.

• t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

class meshmode.mesh.generation.WobblyCircle(coeffs: ndarray)

static random(ncoeffs: int, seed: int)

__call__(t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

class meshmode.mesh.generation.NArmedStarfish(n_arms: int, amplitude: float)

Inherits from WobblyCircle.

__call__(t: ndarray)

Parameters:

t – the parametrization, runs from \([0, 1]\).

Returns:

an array of shape (2, t.size).

Surfaces

meshmode.mesh.generation.generate_icosahedron(r: float, order: int, *, node_vertex_consistency_tolerance: Optional[Union[float, bool]] = None, unit_nodes: Optional[ndarray] = None) → Mesh

meshmode.mesh.generation.generate_cube_surface(r: float, order: int, *, node_vertex_consistency_tolerance: Optional[Union[float, bool]] = None, unit_nodes: Optional[ndarray] = None) → Mesh

meshmode.mesh.generation.generate_sphere(r: float, order: int, *, uniform_refinement_rounds: int = 0, node_vertex_consistency_tolerance: Optional[Union[float, bool]] = None, unit_nodes: Optional[ndarray] = None, group_cls: Optional[type] = None)

Parameters:

• r – radius of the sphere.

• order – order of the group elements. If unit_nodes is also provided, the orders should match.

• uniform_refinement_rounds – number of uniform refinement rounds to perform after the initial mesh was created.

• node_vertex_consistency_tolerance – passed to the Mesh constructor. If False, no checks are performed.

• unit_nodes – if given, the unit nodes to use. Must have shape (3, nnodes).

• group_cls – a MeshElementGroup subclass. Based on the class, a different polyhedron is used to construct the sphere: simplices use generate_icosahedron() and tensor products use a generate_cube_surface().

meshmode.mesh.generation.generate_torus(r_major: float, r_minor: float, n_major: int = 20, n_minor: int = 10, order: int = 1, node_vertex_consistency_tolerance: Optional[Union[float, bool]] = None, unit_nodes: Optional[ndarray] = None, group_cls: Optional[type] = None) → Mesh

Generate a torus.

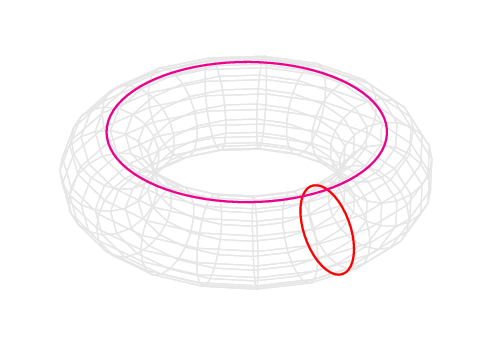
A torus with major circle (magenta) and minor circle (red).

The torus is obtained as the image of the parameter domain \((u, v) \in [0, 2\pi) \times [0, 2 \pi)\) under the map

\[\begin{split}\begin{aligned} x &= \cos(u) (r_\text{major} + r_\text{minor} \cos(v)) \\ y &= \sin(u) (r_\text{major} + r_\text{minor} \sin(v)) \\ z &= r_\text{minor} \sin(v) \end{aligned}\end{split}\]

where \(r_\text{major}\) and \(r_\text{minor}\) are the radii of the major and minor circles, respectively. The parameter domain is tiled with \(n_\text{major} \times n_\text{minor}\) contiguous rectangles, and then each rectangle is subdivided into two triangles.

Parameters:

• r_major – radius of the major circle.

• r_minor – radius of the minor circle.

• n_major – number of rectangles along major circle.

• n_minor – number of rectangles along minor circle.

• order – order of the (simplex) elements. If unit_nodes is also provided, the orders should match.

• node_vertex_consistency_tolerance – passed to the Mesh constructor. If False, no checks are performed.

• unit_nodes – if given, the unit nodes to use. Must have shape (3, nnodes).

Returns:

a Mesh of a torus.

meshmode.mesh.generation.refine_mesh_and_get_urchin_warper(order: int, m: int, n: int, est_rel_interp_tolerance: float, min_rad: float = 0.2, uniform_refinement_rounds: int = 0) → Mesh

Parameters:

• order – order of the (simplex) elements.

• m – order of the spherical harmonic \(Y^m_n\).

• n – order of the spherical harmonic \(Y^m_n\).

• est_rel_interp_tolerance – a tolerance for the relative interpolation error estimates on the warped version of the mesh.

Returns:

a tuple (refiner, warp_mesh), where refiner is a RefinerWithoutAdjacency (from which the unwarped mesh may be obtained), and whose get_current_mesh() returns a locally-refined Mesh of a sphere and warp_mesh is a callable taking and returning a mesh that warps the unwarped mesh into a smooth shape covered by a spherical harmonic of order \((m, n)\).

meshmode.mesh.generation.generate_urchin(order: int, m: int, n: int, est_rel_interp_tolerance: float, min_rad: float = 0.2) → Mesh

Parameters:

• order – order of the (simplex) elements. If unit_nodes is also provided, the orders should match.

• m – order of the spherical harmonic \(Y^m_n\).

• n – order of the spherical harmonic \(Y^m_n\).

• est_rel_interp_tolerance – a tolerance for the relative interpolation error estimates on the warped version of the mesh.

Returns:

a refined Mesh of a smooth shape covered by a spherical harmonic of order \((m, n)\).

meshmode.mesh.generation.generate_surface_of_revolution(get_radius: Callable[[ndarray, ndarray], ndarray], height_discr: ndarray, angle_discr: ndarray, order: int, *, node_vertex_consistency_tolerance: Optional[Union[float, bool]] = None, unit_nodes: Optional[ndarray] = None) → Mesh

Return a cylinder aligned with the “height” axis aligned with the Z axis.

Parameters:

• get_radius – A callable function that takes in a 1D array of heights and a 1D array of angles and returns a 1D array of radii.

• height_discr – A discretization of [0, 2*pi).

• angle_discr – A discretization of [0, 2*pi).

• order – order of the (simplex) elements. If unit_nodes is also provided, the orders should match.

• node_vertex_consistency_tolerance – passed to the Mesh constructor. If False, no checks are performed.

• unit_nodes – if given, the unit nodes to use. Must have shape (3, nnodes).

Volumes

meshmode.mesh.generation.generate_box_mesh(axis_coords, order=1, *, coord_dtype=<class 'numpy.float64'>, periodic=None, group_cls=None, boundary_tag_to_face=None, mesh_type=None, unit_nodes=None) → Mesh

Create a semi-structured mesh.

Parameters:

• axis_coords – a tuple with a number of entries corresponding to the number of dimensions, with each entry a numpy array specifying the coordinates to be used along that axis. The coordinates for a given axis must define a nonnegative number of subintervals (in other words, the length can be 0 or a number greater than or equal to 2).

• periodic – an optional tuple of bool indicating whether the mesh is periodic along each axis. Acts as a shortcut for calling meshmode.mesh.processing.glue_mesh_boundaries().

• group_cls – One of meshmode.mesh.SimplexElementGroup or meshmode.mesh.TensorProductElementGroup.

• boundary_tag_to_face –

  an optional dictionary for tagging boundaries. The keys correspond to custom boundary tags, with the values giving a list of the faces on which they should be applied in terms of coordinate directions (+x, -x, +y, -y, +z, -z, +w, -w).

  For example:

  boundary_tag_to_face={"bdry_1": ["+x", "+y"], "bdry_2": ["-x"]}
  

• mesh_type –

  In two dimensions with non-tensor-product elements, mesh_type may be set to "X" to generate this type of mesh:

  _______
  |\   /|
  | \ / |
  |  X  |
  | / \ |
  |/   \|
  ^^^^^^^
  

  instead of the default:

  _______
  |\    |
  | \   |
  |  \  |
  |   \ |
  |    \|
  ^^^^^^^
  

  Specifying a value other than None for all other mesh dimensionalities and element types is an error.

Changed in version 2017.1: group_factory parameter added.

Changed in version 2020.1: boundary_tag_to_face parameter added.

Changed in version 2020.3: group_factory deprecated and renamed to group_cls.

meshmode.mesh.generation.generate_regular_rect_mesh(a=(0, 0), b=(1, 1), *, nelements_per_axis=None, npoints_per_axis=None, periodic=None, order=1, boundary_tag_to_face=None, group_cls=None, mesh_type=None, n=None) → Mesh

Create a semi-structured rectangular mesh with equispaced elements.

Parameters:

• a – the lower left hand point of the rectangle.

• b – the upper right hand point of the rectangle.

• nelements_per_axis – an optional tuple of integers indicating the number of elements along each axis.

• npoints_per_axis – an optional tuple of integers indicating the number of points along each axis.

• periodic – an optional tuple of bool indicating whether the mesh is periodic along each axis. Acts as a shortcut for calling meshmode.mesh.processing.glue_mesh_boundaries().

• order – the mesh element order.

• boundary_tag_to_face – an optional dictionary for tagging boundaries. See generate_box_mesh().

• group_cls – see generate_box_mesh().

• mesh_type – see generate_box_mesh().

Note

Specify only one of nelements_per_axis and npoints_per_axis.

meshmode.mesh.generation.generate_warped_rect_mesh(dim, order, *, nelements_side=None, npoints_side=None, group_cls=None, n=None) → Mesh

Generate a mesh of a warped square/cube. Mainly useful for testing functionality with curvilinear meshes.

meshmode.mesh.generation.generate_annular_cylinder_slice_mesh(n, center, inner_radius, outer_radius, periodic=False) → Mesh

Generate a slice of a 3D annular cylinder for \(\theta \in [-\frac{\pi}{4}, \frac{\pi}{4}]\). Optionally periodic in $theta$.

Tools for Iterative Refinement

meshmode.mesh.generation.warp_and_refine_until_resolved(unwarped_mesh_or_refiner, warp_callable, est_rel_interp_tolerance) → Mesh

Given an original (“unwarped”) meshmode.mesh.Mesh and a warping function warp_callable that takes and returns a mesh and a tolerance to which the mesh should be resolved by the mapping polynomials, this function will iteratively refine the unwarped_mesh until relative interpolation error estimates on the warped version are smaller than est_rel_interp_tolerance on each element.

Returns:

The refined, unwarped mesh.

New in version 2018.1.

Mesh input/output

class meshmode.mesh.io.ScriptSource(source, extension)

New in version 2016.1.

class meshmode.mesh.io.FileSource(filename)

New in version 2014.1.

class meshmode.mesh.io.ScriptWithFilesSource(source, filenames, source_name='temp.geo')

New in version 2016.1.

source

The script code to be fed to gmsh.

filenames

The names of files to be copied to the temporary directory where gmsh is run.

meshmode.mesh.io.read_gmsh(filename, force_ambient_dim=None, mesh_construction_kwargs=None, return_tag_to_elements_map=False)

Read a gmsh mesh file from filename and return a meshmode.mesh.Mesh.

Parameters:

• force_ambient_dim – if not None, truncate point coordinates to this many dimensions.

• mesh_construction_kwargs – None or a dictionary of keyword arguments passed to the meshmode.mesh.Mesh constructor.

• return_tag_to_elements_map – If True, return in addition to the mesh a dict that maps each volume tag in the gmsh file to a numpy.ndarray containing meshwide indices of the elements that belong to that volume.

meshmode.mesh.io.generate_gmsh(source, dimensions=None, order=None, other_options=None, extension='geo', gmsh_executable='gmsh', force_ambient_dim=None, output_file_name='output.msh', mesh_construction_kwargs=None, target_unit=None, return_tag_to_elements_map=False)

Run gmsh on the input given by source, and return a meshmode.mesh.Mesh based on the result.

Parameters:

• source – an instance of either gmsh_interop.reader.FileSource or gmsh_interop.reader.ScriptSource

• force_ambient_dim – if not None, truncate point coordinates to this many dimensions.

• mesh_construction_kwargs – None or a dictionary of keyword arguments passed to the meshmode.mesh.Mesh constructor.

• target_unit – Value of the option Geometry.OCCTargetUnit. Supported values are the strings ‘M’ or ‘MM’.

meshmode.mesh.io.from_meshpy(mesh_info, order=1)

Imports a mesh from a meshpy mesh_info data structure, which may be generated by either meshpy.triangle or meshpy.tet.

meshmode.mesh.io.from_vertices_and_simplices(vertices, simplices, order=1, fix_orientation=False)

Imports a mesh from a numpy array of vertices and an array of simplices.

Parameters:

• vertices – An array of vertex coordinates with shape (ambient_dim, nvertices)

• simplices – An array (nelements, nvertices) of (mesh-wide) vertex indices.

meshmode.mesh.io.to_json(mesh)

Return a JSON-able Python data structure for mesh. The structure directly reflects the meshmode.mesh.Mesh data structure.

Mesh processing

class meshmode.mesh.processing.BoundaryPairMapping(from_btag: int, to_btag: int, aff_map: AffineMap)

Represents an affine mapping from one boundary to another.

from_btag

The tag of one boundary.

to_btag

The tag of the other boundary.

aff_map

An meshmode.AffineMap that maps points on boundary from_btag into points on boundary to_btag.

meshmode.mesh.processing.find_group_indices(groups, meshwide_elems)

Parameters:

• groups – A list of MeshElementGroup instances that contain meshwide_elems.

• meshwide_elems – A numpy.ndarray of mesh-wide element numbers. Usually computed by elem + base_element_nr.

Returns:

A numpy.ndarray of group numbers that meshwide_elem belongs to.

meshmode.mesh.processing.partition_mesh(mesh: Mesh, part_id_to_elements: Mapping[Hashable, ndarray], return_parts: Optional[Sequence[Hashable]] = None) → Mapping[Hashable, Mesh]

Parameters:

• mesh – A Mesh to be partitioned.

• part_id_to_elements – A dict mapping a part identifier to a sorted numpy.ndarray of elements.

• return_parts – An optional list of parts to return. By default, returns all parts.

Returns:

A dict mapping part identifiers to instances of Mesh that represent the corresponding part of mesh.

meshmode.mesh.processing.find_volume_mesh_element_orientations(mesh, tolerate_unimplemented_checks=False)

Return a positive floating point number for each positively oriented element, and a negative floating point number for each negatively oriented element.

Parameters:

tolerate_unimplemented_checks – If True, elements for which no check is available will return NaN.

meshmode.mesh.processing.flip_simplex_element_group(vertices, grp, grp_flip_flags)

meshmode.mesh.processing.perform_flips(mesh, flip_flags, skip_tests=False)

Parameters:

flip_flags – A numpy.ndarray with meshmode.mesh.Mesh.nelements entries indicating by their Boolean value whether the element is to be flipped.

meshmode.mesh.processing.find_bounding_box(mesh)

Returns:

a tuple (min, max), each consisting of a numpy.ndarray indicating the minimal and maximal extent of the geometry along each axis.

meshmode.mesh.processing.merge_disjoint_meshes(meshes, skip_tests=False, single_group=False)

meshmode.mesh.processing.split_mesh_groups(mesh, element_flags, return_subgroup_mapping=False)

Split all the groups in mesh according to the values of element_flags. The element flags are expected to be integers defining, for each group, how the elements are to be split into subgroups. For example, a single-group mesh with flags:

element_flags = [0, 0, 0, 42, 42, 42, 0, 0, 0, 41, 41, 41]

will create three subgroups. The integer flags need not be increasing or contiguous and can repeat across different groups (i.e. they are group-local).

Parameters:

element_flags – a numpy.ndarray with nelements entries indicating how the elements in a group are to be split.

Returns:

a Mesh where each group has been split according to flags in element_flags. If return_subgroup_mapping is True, it also returns a mapping of (group_index, subgroup) -> new_group_index.

meshmode.mesh.processing.glue_mesh_boundaries(mesh, bdry_pair_mappings_and_tols, *, use_tree=None)

Create a new mesh from mesh in which one or more pairs of boundaries are “glued” together such that the boundary surfaces become part of the interior of the mesh. This can be used to construct, e.g., periodic boundaries.

Corresponding boundaries’ vertices must map into each other via an affine transformation (though the vertex ordering need not be the same). Currently operates only on facial adjacency; any existing nodal adjacency in mesh is ignored/invalidated.

Parameters:

• bdry_pair_mappings_and_tols – a list of tuples (mapping, tol), where mapping is a BoundaryPairMapping instance that specifies a mapping between two boundaries in mesh that should be glued together, and tol is the allowed tolerance between the transformed vertex coordinates of the first boundary and the vertex coordinates of the second boundary when attempting to match the two. Pass at most one mapping for each unique (order-independent) pair of boundaries.

• use_tree – Optional argument indicating whether to use a spatial binary search tree or a (quadratic) numpy algorithm when matching vertices.

meshmode.mesh.processing.map_mesh(mesh, f)

Apply the map f to the mesh. f needs to accept and return arrays of shape (ambient_dim, npoints).

meshmode.mesh.processing.affine_map(mesh, A: Optional[Union[generic, ndarray]] = None, b: Optional[Union[generic, ndarray]] = None)

Apply the affine map \(f(x) = A x + b\) to the geometry of mesh.

meshmode.mesh.processing.rotate_mesh_around_axis(mesh, *, theta: Real, axis: Optional[ndarray] = None)

Rotate the mesh by theta radians around the axis axis.

Parameters:

axis – a (not necessarily unit) vector. By default, the rotation is performed around the \(z\) axis.

Mesh refinement

class meshmode.mesh.refinement.RefinerWithoutAdjacency(mesh)

A refiner that may be applied to non-conforming meshmode.mesh.Mesh instances. It does not generate adjacency information.

Note

If the input meshes to this refiner are not conforming, then the resulting meshes may contain duplicated vertices. (I.e. two different numbers referring to the same geometric vertex.)

__init__(mesh)

refine(refine_flags)

Parameters:

refine_flags – an ndarray of dtype bool and length meshmode.mesh.Mesh.nelements indicating which elements should be split.

refine_uniformly()

get_current_mesh()

get_previous_mesh()

meshmode.mesh.refinement.refine_uniformly(mesh, iterations, with_adjacency=False)

Mesh visualization

meshmode.mesh.visualization.draw_2d_mesh(mesh: Mesh, *, draw_vertex_numbers: bool = True, draw_element_numbers: bool = True, draw_nodal_adjacency: bool = False, draw_face_numbers: bool = False, set_bounding_box: bool = False, **kwargs: Any) → None

Draw the mesh and its connectivity using matplotlib.

Parameters:

• set_bounding_box – if True, the plot limits are set to the mesh bounding box. This can help if some of the actors are not visible.

• kwargs – additional arguments passed to PathPatch when drawing the mesh group elements.

meshmode.mesh.visualization.draw_curve(mesh: Mesh, *, el_bdry_style: str = 'o', el_bdry_kwargs: Optional[Dict[str, Any]] = None, node_style: str = 'x-', node_kwargs: Optional[Dict[str, Any]] = None) → None

Draw a curve mesh.

Parameters:

• el_bdry_kwargs – passed to plot when drawing elements.

• node_kwargs – passed to plot when drawing group nodes.

meshmode.mesh.visualization.write_vertex_vtk_file(mesh: Mesh, file_name: str, *, compressor: Optional[str] = None, overwrite: bool = False) → None

meshmode.mesh.visualization.mesh_to_tikz(mesh: Mesh) → str

meshmode.mesh.visualization.vtk_visualize_mesh(actx: ArrayContext, mesh: Mesh, filename: str, *, vtk_high_order: bool = True, overwrite: bool = False) → None

meshmode.mesh.visualization.write_stl_file(mesh: Mesh, stl_name: str, *, overwrite: bool = False) → None

Writes a STL file from a triangular mesh in 3D. Requires the numpy-stl package.

meshmode.mesh.visualization.visualize_mesh_vertex_resampling_error(actx: ArrayContext, mesh: Mesh, filename: str, *, overwrite: bool = False) → None