Welcome to grudge’s Documentation!#

Here’s an example to solve the PDE

\[\begin{split}\begin{cases} u_t + 2\pi u_x = 0, \\ u(0, t) = -\sin(2\pi t), \\ u(x, 0) = \sin(x), \end{cases}\end{split}\]

on the domain \(x \in [0, 2\pi]\). We closely follow Chapter 3 of [Hesthaven_2008].

import numpy as np
import pyopencl as cl
from grudge.discretization import make_discretization_collection
import grudge.op as op
import grudge.geometry as geo
from grudge.dof_desc import as_dofdesc
from meshmode.mesh.generation import generate_box_mesh
from meshmode.array_context import PyOpenCLArrayContext
from grudge.dof_desc import BoundaryDomainTag, FACE_RESTR_INTERIOR


ctx = cl.create_some_context()
queue = cl.CommandQueue(ctx)
actx = PyOpenCLArrayContext(queue)

nel = 10
coords = np.linspace(0, 2*np.pi, nel)
mesh = generate_box_mesh((coords,),
                         boundary_tag_to_face={"left": ["-x"],
                                               "right": ["+x"]})
dcoll = make_discretization_collection(actx, mesh, order=1)


def initial_condition(x):
    # 'x' contains ndim arrays.
    # 'x[0]' gets the first coordinate value of all the nodes
    return actx.np.sin(x[0])


def left_boundary_condition(x, t):
    return actx.np.sin(x[0] - 2 * np.pi * t)


def flux(dcoll, u_tpair):
    dd = u_tpair.dd
    velocity = np.array([2 * np.pi])
    normal = geo.normal(actx, dcoll, dd)

    v_dot_n = np.dot(velocity, normal)
    u_upwind = actx.np.where(v_dot_n > 0,
                             u_tpair.int, u_tpair.ext)
    return u_upwind * v_dot_n


vol_discr = dcoll.discr_from_dd("vol")
left_bndry = as_dofdesc(BoundaryDomainTag("left"))
right_bndry = as_dofdesc(BoundaryDomainTag("right"))

x_vol = actx.thaw(dcoll.nodes())
x_bndry = actx.thaw(dcoll.discr_from_dd(left_bndry).nodes())

uh = initial_condition(x_vol)

dt = 0.001
t = 0
t_final = 0.5

# timestepper loop
while t < t_final:
    # extract the left boundary trace pair
    lbnd_tpair = op.bv_trace_pair(dcoll,
                                  dd=left_bndry,
                                  interior=uh,
                                  exterior=left_boundary_condition(x_bndry, t))
    # extract the right boundary trace pair
    rbnd_tpair = op.bv_trace_pair(dcoll,
                                  dd=right_bndry,
                                  interior=uh,
                                  exterior=op.project(dcoll, "vol",
                                                      right_bndry, uh))
    # extract the trace pairs on the interior faces
    interior_tpair = op.local_interior_trace_pair(dcoll, uh)
    Su = op.weak_local_grad(dcoll, uh)

    lift = op.face_mass(dcoll,
                        # left boundary weak-flux terms
                        op.project(dcoll,
                                   left_bndry, "all_faces",
                                   flux(dcoll, lbnd_tpair))
                        # right boundary weak-flux terms
                        + op.project(dcoll,
                                     right_bndry, "all_faces",
                                     flux(dcoll, rbnd_tpair))
                        # interior weak-flux terms
                        + op.project(dcoll,
                                     FACE_RESTR_INTERIOR, "all_faces",
                                     flux(dcoll, interior_tpair)))

    duh_by_dt = op.inverse_mass(dcoll,
                                np.dot([2 * np.pi], Su) - lift)

    # forward euler time step
    uh = uh + dt * duh_by_dt
    t += dt

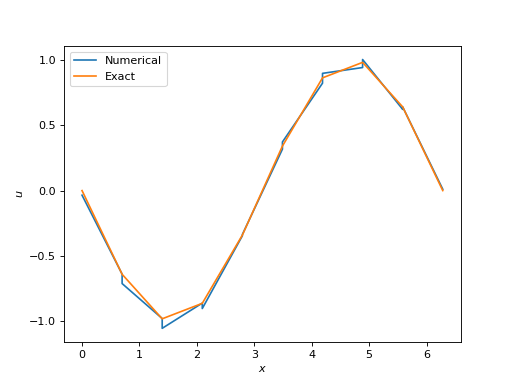
Plotting numerical solution uh in results in

(Source code, png, hires.png, pdf)

Contents:

Welcome to grudge’s Documentation!#

Indices and Tables#