Welcome to modepy’s documentation!¶
modepy helps you create well-behaved high-order discretizations on
simplices (i.e. triangles and tetrahedra) and tensor products of simplices
(i.e. squares, cubes, prisms, etc.). These are a key building block for
high-order unstructured discretizations, as often used in a finite element
context. It closely follows the approach taken in the book
Hesthaven, Jan S., and Tim Warburton. “Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications”. 1st ed. Springer, 2007. Book web page
The basic objects that modepy manipulates are functions on a simplex.
For example, it supplies an orthonormal basis on triangles (shown here) and tetrahedra.
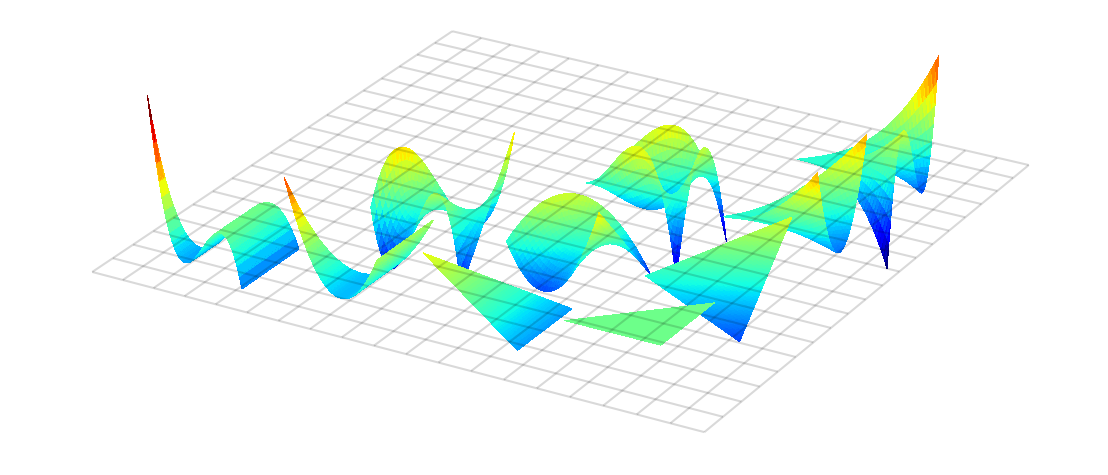
The file that created this plot is included in the modepy distribution
as examples/plot-basis.py.
Here’s an idea of code that uses modepy:
from __future__ import annotations
import numpy as np
import modepy as mp
# Define the shape and function space on which we will operate
n = 17 # use this total degree
dimensions = 2
shape = mp.Simplex(dimensions)
space = mp.PN(dimensions, n)
# Get a basis of orthonormal functions and some nodes.
basis = mp.orthonormal_basis_for_space(space, shape)
nodes = mp.edge_clustered_nodes_for_space(space, shape)
x, y = nodes
# We want to compute the x derivative of this function:
f = np.sin(5*x + y)
df_dx = 5 * np.cos(5*x + y)
# The (generalized) Vandermonde matrix transforms coefficients into
# nodal values. So we can find basis coefficients by applying its
# inverse:
vdm = mp.vandermonde(basis.functions, nodes)
f_coefficients = np.linalg.solve(vdm, f)
# Now linearly combine the (x-)derivatives of the basis using
# f_coefficients to compute the numerical derivatives.
dx = mp.multi_vandermonde(basis.gradients, nodes)[0]
df_dx_num = dx @ f_coefficients
assert np.linalg.norm(df_dx - df_dx_num) < 1.0e-5
This file is included in the modepy distribution as
examples/derivative.py.