Flux Specification Language¶
Summary¶
An “flux expression” is an expression tree that represents a numerical DG flux. Flux expressions may be passed to hedge.optemplate.get_flux_operator() to integrate with the Operator Specification Language. The following components can be used to build flux expressions in hedge:
Scalar constants, may be of type int, float, complex, numpy.number. These occur directly as part of the expression tree. pymbolic.primitives.is_constant() is a predicate to test for constant-ness.
numpy.ndarray with dtype=:class:`object` (called “object array” in numpy-speak). When processed by hedge.optemplate.get_flux_operator(), vector fluxes result in an object array of scalar fluxes.
Use hedge.tools.join_fields() to easily create object arrays from scalars and other arrays.
Normal represents one axial (i.e. x, y or z) component of the face normal for which the flux is to be computed.
Use make_normal() to generate an object array of normal components for more natural, vectorial use of the normal.
FieldComponent allows access to the DG-discretized fields for which the flux is to be computed. If the flux operator is bound to a scalar field, it refers to it by the index 0. If it is bound to a vector field, indices are subscripts into this vector field.
Further, FieldComponent lets you specify which side of an element interface the placeholder stands by its is_interior parameter.
PenaltyTerm: Evaluates to the conventional penalty term
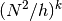 , where the power
, where the power 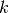 is adjustable
by the user,
is adjustable
by the user, 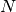 represents the order of the discretization,
and
represents the order of the discretization,
and  represents the surface Jacobian.
represents the surface Jacobian.pymbolic.primitives.Sum, pymbolic.primitives.Product, pymbolic.primitives.Quotient, pymbolic.primitives.Power: These are created implicitly when Expression objects are combined using the +, -, *, / and ** operators. These are all interpreted in a node-by-node fashion.
pymbolic.primitives.IfPositive offers a simple way to build conditionals and is interpreted in a node-by-node fashion.
pymbolic.primitives.CommonSubexpression (CSE for short): Prevents double evaluation of identical subexpressions when the flux expression tree is walked to evaluate the operator.
Use hedge.optemplate.primitives.make_common_subexpression() to wrap each component of an object array in a CSE.
hedge.flux.FluxScalarParameter: A placeholder for a user-supplied scalar value, drawn from the same namespace as hedge.optemplate.ScalarParameter.
pymbolic.primitives.Call: The function attribute must evaluate to one of a number of predefined pymbolic.primitive.FunctionSymbol instances or be a value of type hedge.optemplate.primitives.CFunction.
See also
Simplifying Flux Notation with Placeholders¶
Suppose the state vector ![[u,v_x,v_y]](_images/math/a0f4b7f46d5cc071fa934bf65ded7bd0f5f028ee.png) is contained
in the variable q and the flux to be calculated is
is contained
in the variable q and the flux to be calculated is
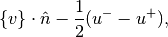
using the convetional flux notation (see Hesthaven/Warburton, “Nodal Discontinuous Galerkin Methods”).
Then this can be expressed as:
flux = 0.5* (
(FieldComponent(1, True) + FieldComponent(1, False)) * Normal(0)
+ (FieldComponent(2, True)+ FieldComponent(2, False)) * Normal(1)
- (FieldComponent(0, True) - FieldComponent(0, False))
)
and the flux is then bound to the components of q using:
get_flux_operator(flux)*q
This is however rather cumbersome. We may use FluxVectorPlaceholder to simplify the notation.
We begin by introducing flux placeholders, specifying that our state vector contains three components, as above, and extract slices to get symbolic, vectorial representations of u, v, and the normal:
q_ph = FluxVectorPlaceholder(3)
u = q_ph[0]
v = q_ph[1:]
n = make_normal(2) # normal has two dimensions
Then the flux simplifies to:
flux = numpy.dot(v.avg, n) - 0.5*(u.int - u.ext)
The resulting flux expression will be the same as above, but notational effort is greatly reduced.